Parte IV – El discreto encanto de la trigonometría.
Como hemos visto en la sección anterior, el método LSB (Low Significant Bit), se detecta con facilidad analizando el espectro luminoso de la imagen.
Es, por tanto, un método indiscreto.
El título de esa sección ya te da la pista de cómo vamos a mejorar el procedimiento de ocultación.

Vamos a ver ahora un método algo más discreto, es decir, que pase más desapercibido. Y qué mejor discreción que usar el método TDC, es decir, la Transformada Discreta del Coseno.
Para entender este método primero debemos saber cómo se codifica una imagen JPG.
Una de las diferencias entre el formato JPG y otros formatos gráficos (como PPM, PNG, BMP, TIF) es que JPG es un formato en el que se pierde información de la imagen. Lo importante es conseguir que la pérdida de información no sea apreciable al ojo (bueno, al cerebro, porque es quien ve en realidad).
Los otros formatos almacenan la información en RGB (Rojo, Verde, Azul). JPG almacena la información también en tres componentes, pero esos componentes son la Luminancia, la imagen en tonos de grises (Y), y dos componentes de color (Cb y Cr).
El paso del sistema RGB al de YCbCr se realiza mediante unas simples ecuaciones:
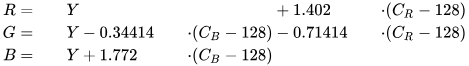
Como nuestro ojo es mucho más sensible a las diferencias de luminosidad (niveles de grises) que a los niveles de color (como bien sabemos los que observamos el cielo de noche) es posible reducir el espacio dedicado a la información de color, dejando más espacio para la Luminancia.
Ahora es donde aparece nuestro amigo, el coseno. La Transformada Discreta del Coseno (TDC). La Transformada Discreta del Coseno es un caso particular de la Transformada Discreta de Fourier que a su vez es un caso particular de la Transformada de Fourier.
Con las Matemáticas hemos topado, amigo Sancho.
He estado pensando bastante cómo describir en qué consiste la TDC sin necesidad de recurrir a las matemáticas.
Voy a intentar explicar el significado físico de la transformada de Fourier porque si te pongo directamente su expresión matemática vas a dejar de leer.
He extraído una escena de la fabulosa película de Milos Forman, Amadeus.
Visualiza primero este vídeo:
Probablemente, el vídeo con esas imágenes y textos superpuestos no te diga nada. Así que voy a intentar explicarlo de un modo sencillo:
En el vídeo vemos a Mozart caminando hacia la sala donde el Emperador José intenta, con gran dificultad, interpretar una pieza de bienvenida compuesta por Salieri.
Wolfgang escucha atentamente el sonido. Pero, ¿qué es realmente ese sonido? Es energía que se transmite en forma de variaciones de presión del aire. La transmisión de esa energía se hace en forma de ondas cuya amplitud cambia con el tiempo.
Mozart, con su extraordinario oído, es capaz de captar en esa onda las notas que emite el clave (o clavicordio). Es decir, identifica las frecuencias individuales que componen la melodía. Cada nota musical se corresponde con una frecuencia pura. Así, sin saberlo, Mozart realiza en su mente lo que matemáticamente se conoce como una transformada de Fourier.
La transformada de Fourier permite descomponer una señal compleja (como una melodía) en sus componentes más simples: ondas puras. Es como descubrir los ingredientes de un plato probándolo (esta metáfora quizás es poco fidedigna, pero creo que aplica al ejemplo).
Esos “ingredientes” son ondas simples que pueden describirse mediante funciones seno y coseno. Cuanto más compleja sea la música, más funciones necesitaremos para describirla. El sonido que escucha Mozart puede representarse como una suma de estas ondas seno y coseno, cada una con un coeficiente que indica su “peso” en la mezcla.
La transformada de Fourier utiliza una suma infinita de estas funciones. Pero existen versiones más manejables, como la Transformada Discreta del Coseno (TDC), que nos permite aproximar una señal compleja usando solo un número finito de funciones coseno. Esto es especialmente útil en aplicaciones como la compresión de audio e imagen.
En resumen: estas transformaciones nos permiten pasar del dominio del tiempo o del espacio al dominio de las frecuencias, revelando la estructura oculta de las señales que percibimos.
Podemos aplicarla a funciones que toman valores en más dimensiones. Por ejemplo, en una imagen: a cada píxel (par de valores o coordenadas x e y) se asocia el valor (o valores RGB) de la intensidad de color.
Al aplicar la transformada TDC a esa función, obtenemos las frecuencias espaciales que componen la imagen, es decir, sus elementos fundamentales.
¿Por qué pasar al dominio de la frecuencia? Porque nos permitirá descartar los componentes de frecuencias más altas que, aunque aportan información de la fotografía, pasan desapercibidos en la visión de la imagen. Hay que llegar a un compromiso en la eliminación de frecuencias altas (que son las responsables del detalle de la foto) para que no se quede una imagen borrosa.
Recuerda que las imágenes no son más que un mosaico de píxeles. Para realizar los cálculos de la TDC la imagen se divide en bloques de 8 * 8 píxeles. Lo que nos dará la transformada es un conjunto de 64 elementos. Cada uno de esos elementos representa el peso de cada una de las frecuencias fundamentales que se obtienen de la imagen.
A ver si me explico…
En la imagen siguiente se representan las funciones coseno que, convenientemente moduladas por coeficientes, permiten obtener cualquier imagen compuesta de un cuadrado de 8 * 8 píxeles.

No sé si te estoy pidiendo un acto de fe…
A ver si con este esquema que he preparado se ve más claro

① El proceso de compresión JPG comienza con una matriz de 8*8 píxelws (correspondiente a uno de los bloques en que se divide una imagen).
② Al aplicar la TDC a esa matriz obtenemos otra matriz semejante ③ con coeficientes distintos que son los pesos de cada función coseno (Imagen 1) que permiten construir la imagen.
Antes de decidir qué frecuencias eliminamos para reducir la imagen, hay que realizar un proceso de cuantización. Para ello se utiliza una matriz especial ④ diseñada para que la imagen resultante tenga la calidad que buscamos. Seguramente cuando has editado una imagen JPG en un programa de edición has elegido con qué calidad almacenas la imagen. Ahí estás decidiendo qué matriz de cuantización usar.
La matriz de cuantización ④ dará prioridad a los elementos de baja frecuencia de la imagen respecto a los de alta frecuencia.
⑤ El proceso de cuantización consiste en dividir uno a uno cada elemento de la matriz TDC ③ por el elemento correspondiente de la matriz de cuantización ④. Así obtenemos la matriz cuantizada ⑥.
Si observas la matriz ⑥ observarás que la distribución de los valores significativos no es aleatoria. La mayor parte de la información de la imagen aparece en la esquina superior izquierda (bajas frecuencias) mientras que en la esquina inferior derecha (altas frecuencias) los coeficientes son casi nulos.
⑦ El siguiente paso es reordenar la matriz para convertirla en una tupla (pasamos de una matriz de [8,8] a una tupla de [1,64] ⑧. Pero el orden de selección es muy particular (lo he dibujado en el gráfico). El motivo de esa selección en zigzag es que todos los ceros provenientes de las altas frecuencias aparezcan seguidos al final de la tupla unidimensional.
A la secuencia numérica obtenida ⑧ se le va a aplicar una codificación Huffman ⑨. La codificación Huffman resulta muy conveniente para comprimir cadenas de datos. Asigna códigos en función de la frecuencia de aparición de los símbolos de la cadena. Quédate con que se comprime mucho la secuencia de bits a almacenar y si quieres profundizar en el tema la Wikipedia es un buen punto donde ir.
Ya sabes cómo es la estructura interna de un archivo JPG y cómo se construye.
¿Dónde escondemos nuestra firma digital?
Espero que hayas acertado con la respuesta.
En la sección anterior ya te di una pista. ¿Recuerdas?
El método LSB escondía los datos en el bit menos significativo de uno de los componentes de color. Información que se perdía si convertías la imagen a JPG…
La solución que evitara esa pérdida al comprimir JPG es que codificaremos el mensaje (nuestra firma digital) en el bit menos significativo de uno de los coeficientes de la matriz TDC de modo que pasará desapercibido en el espectro de la imagen (como ocurría en e método LSB) y será resistente a la compresión inherente JPG.
Si has llegado hasta aquí estás listo para entender el programa que realizará el proceso.
«Esteganografiar» por el método TDC.
En esta entrada ya he puesto programas y comandos en Powershell, en Openssl y en Perl. Para que no te relajes ahora lo voy a hacer en Python.
Lo que quiero que quede claro es que el lenguaje en el que programas es secundario. Elegiremos uno u otro en función de las librerías que tenga accesibles.
Al igual que en el caso anterior no los voy a pegar, sino que iré poniendo bloques para comentarlos.
Para poder ejecutar este programa tendrás que tener instalado Python (en tu Windows o en tu Linux pues el programa funciona en cualquiera de los dos sistemas operativos).
En primer lugar, cargaremos las librerías que nos ayudaran con los archivos JPG y nos hagan las transformadas discretas del coseno (¿no pensarías que las íbamos a programar?).
import cv2 # Librería para tratar imágenes y la TDC
import numpy as np # Librería para poder operar matrices
import argparse # Librería que permite pasar parámetros al programa
import os # Librería para tratar archivos en el S.O.Un bloque de definición
Q = np.array([
[16,11,10,16,24,40,51,61],
[12,12,14,19,26,58,60,55],
[14,13,16,24,40,57,69,56],
[14,17,22,29,51,87,80,62],
[18,22,37,56,68,109,103,77],
[24,35,55,64,81,104,113,92],
[49,64,78,87,103,121,120,101],
[72,92,95,98,112,100,103,99]
], dtype=np.float32)Habrás reconocido la definición de la matriz de cuantización ④. Es la que aplicaremos en la Luminancia del archivo JPG contenedor del mensaje.
El siguiente bloque definimos tres funciones que utilizaremos en el proceso de inserción y extracción del mensaje
def text_to_bitstring(text):
# Convierte un texto a bits
# Añade un byte nulo (00000000) al final como terminador
return ''.join(f'{ord(c):08b}' for c in text) + '00000000' # Null terminator
def bitstring_to_bytes(bits):
# Convierte una cadena de bits en bytes (texto)
return bytes(int(bits[i:i+8], 2) for i in range(0, len(bits), 8))El bloque principal es muy sencillo:
if __name__ == '__main__':
parser = argparse.ArgumentParser()
parser.add_argument('--input', default='entrada.jpg', help='Imagen original')
parser.add_argument('--output', default='salida.jpg', help='Imagen de salida')
parser.add_argument('--coefx', type=int, default=3, help='Índice X del coeficiente DCT')
parser.add_argument('--coefy', type=int, default=3, help='Índice Y del coeficiente DCT')
parser.add_argument('--msgfile', default='mensaje.txt', help='Archivo de texto a insertar')
parser.add_argument('--quality', type=int, default=100, help='Calidad jpg del archivo de salida')
args = parser.parse_args()
if not os.path.isfile(args.msgfile):
print(f"[ERROR] No se encontró el archivo de mensaje: {args.msgfile}")
exit(1)
success = embed_message(args.input, args.output, args.msgfile, args.coefx, args.coefy, args.quality)
if success:
extract_message(args.output, args.coefx, args.coefy)El programa está preparado para recibir como parámetros varios datos para que pueda ser invocado en scripts.
Los parámetros –input y –output son los archivos de imagen de entrada y salida.
Los parámetros –coefx y –coefy son las coordenadas del coeficiente de la matriz TDC donde insertaremos el mensaje. Lo he dejado configurable para que probéis cómo influye en qué coeficiente metes el mensaje oculto. Juega con él y verás si influye el tipo de imagen en la que queremos ocultar el mensaje.
–msgfile es el nombre del archivo con la firma digital. El contenido del archivo puede ser cualquier cosa, evidentemente.
–quality es la calidad con la que se graba el archivo de salida. Recuerda menor calidad, menor tamañao pero entonces igual se pierde el mensaje. Podrás variar este parámero y sorprenderte hasta donde aguanta el algoritmo.
El programa está preparado para insertar el mensaje y para extraerlo. Siempre puedes modificarlo para separar ambas funciones en dos programas distintos.
Insertando el mensaje.
Vamos a la madre del cordero, la función embed_message:
def embed_message(image_path, output_path, msg_path, coef_x, coef_y, quality):
# ABRE EL ARCHIVO input COMO IMAGEN
img = cv2.imread(image_path, cv2.IMREAD_COLOR)
if img is None:
print(f"[ERROR] No se pudo cargar la imagen: {image_path}")
return False
# ABRE EL MENSAJE DE TEXTO Y LO CONVIERTE A STREAM DE BITS
with open(msg_path, 'r', encoding='utf-8') as f:
text = f.read()
msg_bits = text_to_bitstring(text)Separa los componentes de Luminancia y Crominancia de la imagen. Recuerda que insertaremos el mensaje en la Luminancia.
img_ycc = cv2.cvtColor(img, cv2.COLOR_BGR2YCrCb)
# SEPARACIÓN DE LUMINANCIA Y CROMINANCIA
Y, Cr, Cb = cv2.split(img_ycc)
Y_embed = np.float32(Y.copy())
# TAMAÑO EN PIXELS DE LA IMAGEN CONTENEDORA
height, width = Y.shapeRecorremos la imagen en bloque de 8 * 8 bits
for i in range(0, height - 8, 8):
for j in range(0, width - 8, 8):
if bit_idx >= len(msg_bits):
break
# BIT CORRESPONDIENTE DEL MENSAJE A OCULTAR
bit = int(msg_bits[bit_idx])
# BLOQUE DE 8*8
block = Y_embed[i:i+8, j:j+8]
# TRANSFORMADA DISCRETA DEL COSENO DEL BLOQUE
dct_block = cv2.dct(block)
# CUANTIZACIÓN DE LA MATRIZ DCT (DIVIDIMOS POR ④)
q_block = np.round(dct_block / Q).astype(np.int32)
# SELECCIÓN DEL COEFICIENTE DEFINIDO EN LOS PARAMETROS DE EJECUCION
coef = q_block[coef_y, coef_x]
# EVALUACIÓN BIT MENOS SIGNIFICATIVO DEL COEFICIENTE
lsb = coef & 1
# SI EL BIT LSB NO ES IGUAL AL QUE QUEREMOS INSERTAR LO CAMBIAMOS
if lsb != bit:
coef += 1 if bit == 1 else -1
q_block[coef_y, coef_x] = coef
# DESHACEMOS LA CUANTIZACIÓN (MULTIPLICAMOS POR ④)
dct_block_mod = q_block * Q
# APLICAMOS LA INVERSA DE LA TRANSFORMADA DISCRETA DEL COSENO
Y_embed[i:i+8, j:j+8] = cv2.idct(dct_block_mod)
# SEGUIMOS RECORRIENDO BLOQUES HASTA QUE ACABE EL MENSAJE
bit_idx += 1
if bit_idx >= len(msg_bits):
breakTras haber insertado el mensaje ya podemos reconstruir la imagen contenedora.
# ASEGURAMOS QUE LA LUMINANCIA ESTÁ EN VALORES (0,255)
Y_embed = np.clip(Y_embed, 0, 255).astype(np.uint8)
# COMBINAMOS NUEVA LUMINANCIA CON CROMINANCIAS ORIGINALES
merged = cv2.merge([Y_embed, Cr, Cb])
# CONVERTIMOS A BGR Y SE GUARDA CON LA CALIDAD DEFINIDA EN EL PARÁMETRO DE ENTRADA
result = cv2.cvtColor(merged, cv2.COLOR_YCrCb2BGR)
cv2.imwrite(output_path, result, [int(cv2.IMWRITE_JPEG_QUALITY), quality])
print(f"[INFO] Imagen esteganografiada guardada: {output_path}")
return True¡Y mensaje insertado!
Extrayendo el mensaje.
Todo mensaje oculto debe poder ser desocultado.
Para eso tenemos la función extract_message
def extract_message(image_path, coef_x, coef_y):
stego = cv2.imread(image_path, cv2.IMREAD_COLOR)
if stego is None:
print(f"[ERROR] No se pudo cargar la imagen esteganografiada: {image_path}")
return
height, width, _ = stego.shape
img_ycc = cv2.cvtColor(stego, cv2.COLOR_BGR2YCrCb)
Y = np.float32(cv2.split(img_ycc)[0])
Hay que tener en cuenta que, ya que somos nosotros mismos los que vamos a querer validar un mensaje, debemos recordar en qué posición (coeficiente) hemos dejado los bits…
En ese trozo de código leemos la imagen y separamos la Luminancia (recuerda, la función embed_message).
El código para extraer los bits es muy sencillo:
for i in range(0, height - 8, 8):
for j in range(0, width - 8, 8):
# BLOQUE de 8*8
block = Y[i:i+8, j:j+8]
# TDC DEL BLOQUE
dct_block = cv2.dct(block)
# CUANTIZACIÓN
q_block = np.round(dct_block / Q).astype(np.int32)
# SELECCIÓN COEFICIENTE
coef = q_block[coef_y, coef_x]
# EVALUACIÓN BIT y ALMACENADO
bits += str(coef & 1)
# SI ENCONTRAMOS LA CADENA FINAL -> SE ACABÓ
if bits.endswith('00000000'):
bits = bits[:-8]
breakExtraída la cadena de bits solo resta converitrlos a bytes, es decir, a caracteres:
message = ''
for i in range(0, len(bits), 8):
byte = bits[i:i+8]
if len(byte) < 8:
break
message += chr(int(byte, 2))
print(f"\n[MENSAJE EXTRAÍDO]\n{message}")Y como el movimiento se demuestra andando: aquí un ejemplo de ejecución introduciendo el mensaje en el coeficiente (4,4) y guardando con muy baja calidad (40%):
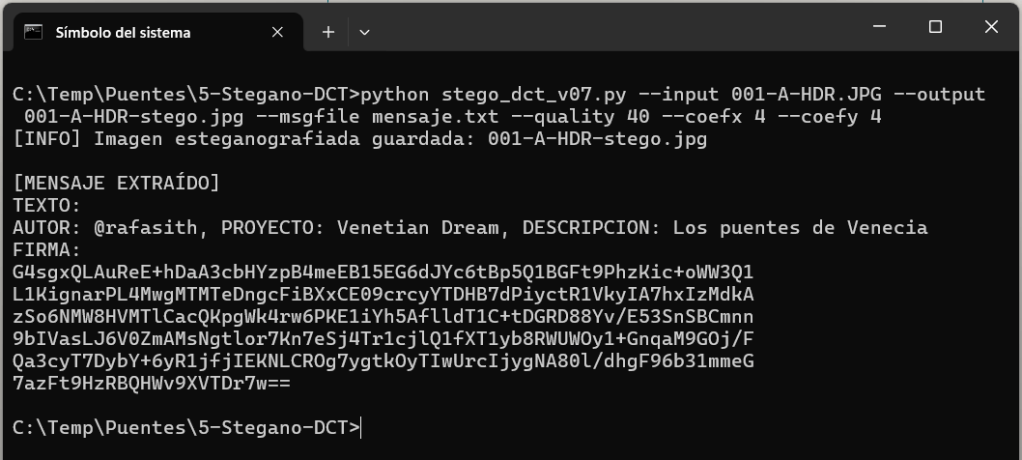
Sí. Ya te has fijado que hay 7 versiones.
Te dejo la comparativa de las dos imágenes:


Y de sus espectros:

Todavía se puede apreciar que hay “algo raro” ¿verdad? Puedes jugar cambiando el coeficiente y la calidad de imagen para ver que en algunos pasa más desapercibida la información insertada.
Hay toda una rama matemática asociada al análisis esteganográfico de imágenes para descubrir si esas inocentes imágenes que circulan por la red llevan en realidad mensajes entre personas.
El programa que he comentado no quiere ser una herramienta, sino un camino para aprender y mejorar. Ni está libre de bugs ni se da con garantías. Pero seguro que te ha abierto la mente.




Deja un comentario